What has the positional “embedding” learned?
In recent years, the powerful Transformer models have become standard equipment for NLP tasks, the usage of positional embedding/encoding has also been taken for granted in front of these models as a standard component to capture positional information. In the original encoder-decoder Transformer model for machine translation (Vaswani et al. 2017), the positional “encoding” uses sinusoidal waves to fill the positional “encoding” weight matrix. It somehow makes sense to present position information in sin/cos waves, as different frequencies are used in different dimensions, as shown in the figure.
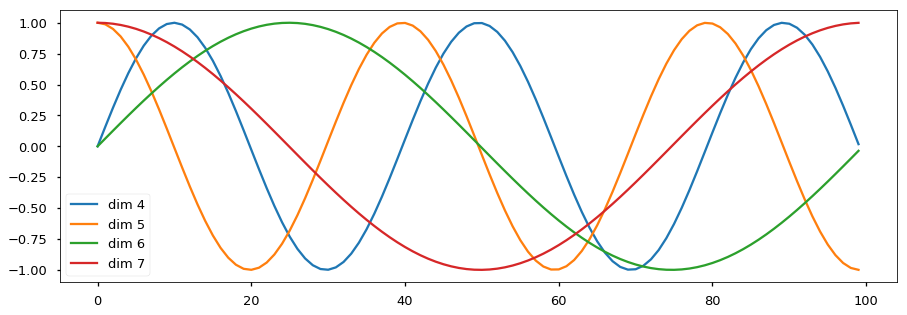
source: http://nlp.seas.harvard.edu/images/the-annotated-transformer_49_0.png
However, for many Transformer-encoder-based pretrained models (BERT, XLNet, GPT-2… in 2018~2019), a fully-learnable matrix is used as positional “embedding” to take place the sinusoidal waves. The way to train the positional embedding is just like we train a normal word embedding layer. Each row in the embedding matrix is independent, no matter what position index is presented. Up to now, there is few discussion about what is learned by the positional embeddings.
Because I wondered whether positional “embedding” learned physical meaning or it was only manipulated by black-box parameters, I do some small experiments to probe the positional “embedding” matrix:
Regression
I trained a linear regression model with the input = vector from positional embedding, output = scaler according to the position.
BERT
bert-base-cased is used. The model was trained for 10000 epochs.
The training set is the vectors with even position, that is, [2*x for x in range(position_size//2)].
The result of the regression model that tested on all even/odd position shows that BERT’s positional embedding poorly model the positional information, especially for the position > 400.

X: the position of the input vector
Y: predicted scaler for input
I also trained a model with the training set equal to the whole vector (even and odd), however, the result shows little change.

X: the position of the input vector
Y: predicted scaler for input
I think that the poor results for position > 400 are because the original BERT implementation does not fill each batch with full sequences with length=512. (But Roberta does it.)
Roberta
The same experiment on Roberta, with training set equal to the even vectors:

X: the position of the input vector
Y: predicted scaler for input
Training set equal to all even+odd vectors:

X: the position of the input vector
Y: predicted scaler for input
The results are better than BERT’s.
GPT-2
The same experiment on GPT-2, with training set equal to the even vectors:

Training set equal to all even+odd vectors:

GPT-2 has a longer positional embedding size (1024). I think that the good results of GPT-2 are caused by left-to-right language modeling. The GPT-2 model needs to be more sensitive to the position of the input vectors. On the other hand, the masked language modeling task (BERT and Roberta) can rely on more bag-of-words information in the sentence. Positional information is not as important to BERT in its task.